Немного истории.
При изучении изменяющихся величин очень часто возникает вопрос о скорости, о быстроте происходящего изменения. Так мы говорим о скорости движения самолета, поезда, автобуса, ракеты, о скорости падения камня, вращения шкива и т.д. Можно говорить о скорости выполнения определенной работы, о скорости протекания химической реакции, о быстроте роста населения в данном городе. О скорости можно говорить по отношению к любой величине, которая изменяется с течением времени. Для всего этого используется понятие производной.
Метод дифференциального исчисления был создан в XVII и XVIII вв. С возникновением этого метода связаны имена двух великих математиков – И. Ньютона и Г.В. Лейбница.
Производная - одно из фундаментальных понятий математики. Оно возникло в 18 веке. Независимо друг от друга И. Ньютон и Г. Лейбниц разработали теорию дифференциального исчисления.
Исаак Ньютон (1643-1727) - один из создателей дифференциального исчисления. Главный его труд - "Математические начала натуральной философии" - оказал колоссальное влияние на развитие естествознания, стал поворотным пунктом в истории естествознания.
Ньютон ввёл понятие производной, изучая законы механики, тем самым раскрыл её механический смысл. Он заключается в следующем: скорость движения материальной точки в данный момент времени равна производной пути по времени, т.е. Таким образом, если закон движения материальной точки задан уравнением, то для нахождения мгновенной скорости точки в какой-нибудь определённый момент времени нужно найти производную и подставить в неё соответствующее значение t.
Г.В. Лейбниц. (1646-1716) - создатель Берлинской академии наук. Основоположник дифференциального исчисления, ввёл большую часть современной символики математического анализа.
Лейбниц пришёл к понятию производной, решая задачу проведения касательной к произвольной линии, объяснив этим ее геометрический смысл.
Но это не говорит о том, что до них эти вопросы не изучались. Задолго до этого Архимед (287 до н.э. - 212 до н. э) не только решил задачу на построение касательной к такой сложной кривой, как спираль, применяя при этом предельные переходы, но и сумел найти максимум функции.
Большой вклад в изучение дифференциального исчисления внесли Лопиталь (1661-1704), Бернулли (1744-1807), Лагранж (1736-1813), Гаусс (1777-1855), Коши (1789-1857). Необходимо сказать, что ни Ньютон, ни Лагранж не дали четкого определения производной. Впервые определение производной было сформулировано Коши, и именно это определение стало общепринятым и в настоящее время используется почти во всех курсах анализа.
Производная в физике
Физические производные величины:
?(t) = х/(t) – скорость
a (t)=?/ (t) - ускорение
J (t) = q/(t) - сила тока
C(t) = Q/(t) - теплоемкость
d(l)=m/(l) - линейная плотность
K (t) = l/(t) - коэффициент линейного расширения
? (t)= ?/(t) - угловая скорость
а (t)= ?/(t) - угловое ускорение
N(t) = A/(t) – мощность
Задача. Автомобиль приближается к мосту со скоростью 72 км/ч. У моста висит дорожный знак "36 км/ч". За 7 сек до въезда на мост, водитель нажал на тормозную педаль. С разрешаемой ли скоростью автомобиль въехал на мост, если тормозной путь определяется формулой s=20t-t
Решение.
v(t) = s/ (t)= 20 – 2t = 20 – 2*7 = 6 (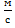 
)
Да, т.к. скорость через 7 с. будет равна 6м/с (21,6 км/ч).
Задача. Количество электричества, протекающее через проводник, задаётся формулой
q(t) = t+4/t. В какой момент времени ток в цепи равен нулю?
Решение:
I(t) = q / (t),
I(t) = 1 - 4/t2
1 - 4/t2 =0
Отсюда, t = 2 или t = 2; t = -2 не подходит по условию задачи
Производная в экономике:
Экономика – основа жизни, а в ней важное место занимает дифференциальное исчисление – аппарат для экономического анализа. Базовая задача экономического анализа – изучение связей экономических величин в виде функций.
Производная в экономике решает важные вопросы:
1. В каком направлении изменится доход государства при увеличении налогов или при введении таможенных пошлин?
2. Увеличится или уменьшится выручка фирмы при увеличениb цены на её продукцию?
В экономике очень часто требуется найти наилучшее или оптимальное значение показателя: наивысшую производительность труда, максимальную прибыль, максимальный выпуск, минимальные издержки и т. д. Каждый показатель представляет собой функцию от одного или нескольких аргументов. Таким образом, нахождение оптимального значения показателя сводится к нахождению экстремума функции.
Производная в экономических формулах:
П (t) = V / (t) - производительность труда,
где V (t) - объем продукции
J(x) = y / (x) - предельные издержки производства,
где y– издержки производства в зависимости от объема выпускаемой продукции x.
Задача. Оборот предприятия за истекший год описывается через функцию
U (t) =0,15t3- 2t2 + 200, где t - месяцы, U-миллионы. оборот предприятия за 9 и 10 месяцы.
Решение. Исследуем оборот предприятия с помощью производной:
U' (t) =0,45t2 - 4t
Меньший оборот был на девятом месяце - 0,45. На 10 месяце - 5.
Задача. Объем продукции V цеха в течение дня зависит от времени по закону
V(t) = -5/3t3+15/2t2+50t+70, где 1 <= t <= 8
Вычислите производительность труда П при t =7 ч.
Решение:
П (t) = V / (t)
П (t) = -5t2+ 15t + 50
П (7) = -5*49 + 15*7 + 50 = - 90 (ед/ч)
Производная в химии
И в химии нашло широкое применение дифференциальное исчисление для построения математических моделей химических реакций и последующего описания их свойств.
Химия - это наука о веществах, о химических превращениях веществ.
Химия изучает закономерности протекания различных реакций.
Скоростью химической реакции называется изменение концентрации реагирующих веществ в единицу времени.
Так как скорость реакции v непрерывно изменяется в ходе процесса, ее обычно выражают производной концентрации реагирующих веществ по времени.
|
Понятие на языке химии |
Обозначение |
Понятие на языке математики |
|
Количество в-ва в момент времени |
p = p(t0) |
Функция |
|
Интервал времени |
?t = t– t0 |
Приращение аргумента |
|
Изменение количества в-ва |
?p= p(t0+ ? t ) – p(t0) |
Приращение функции |
|
Средняя скорость химической реакции |
?p/?t |
Отношение приращения функции к приращению аргумента |
Задача. Пусть количество вещества, вступившего в химическую реакцию, задается зависимостью: р(t) = t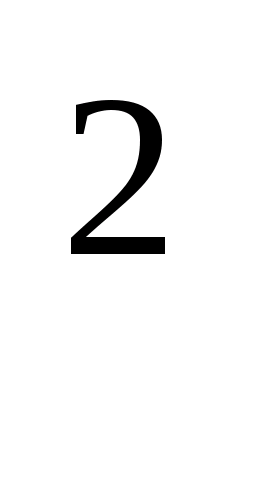 
/2 + 3t –3 (моль). Найти скорость химической реакции через 3 секунды.
Решение:
V (t) = p' (t)= t + 3
V(3)= 3+3=6 (моль/с)
Задача. Определить скорость радиоактивного распада, если задан закон радиоактивного распада N (t)=N0 e-?t , где ?=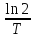 
, N0 = 106, T – период полураспада
Решение: N`(t)=(N0 e-?t)` = N0 e-?t(--?t)`= -? N0 e-?t
Какие необходимы данные для получения числового значения?
Биологический смысл производной.
Пусть зависимость между числом особей популяции микроорганизмов у и временем t её размножения задана уравнением: у=p(t). Пусть ?t-промежуток времени от некоторого начального значения t до t+?t. Тогда у+?у=p(t+?t)- новое значение численности популяции, соответствующее моменту t+?t, а ?y+p(t+?t)-p(t)-изменение числа особей организмов.
Задача. Рассчитайте на основании имеющихся данных, как будет меняться плотность популяции синиц через год и 2 года, если плотность синиц составляет 260 особей/га. За период размножения из одной кладки яиц в среднем выживает 3 детеныша. В популяции равное число самцов и самок. Смертность синиц постоянна, в среднем за год погибает 27% особей. Найти скорость роста численности популяции в год.
Решение: Плотность популяции – это численность популяции на единицу площади. Тогда N0 = 260 особей/га. По условию, в популяции равное число самцов и самок, а значит эффективная численность Ne популяции, равна Ne=100.
Ne = 100 Ne = 1
Коэффициент смертности Ксмер = 27% = 0,27
За год 130 пар дает 390 птенцов, т.е. (260/2)*3 =390
Формула N1= (Ne - Ксмер )( Крожд + N0 ) =(1-0.27)(390+260)= 474 особей за первый год.
Относительный прирост численности популяции ?N= 474/260= 1,82 раза Тогда численность популяции в любой год t задается функцией
N(t)= 260* 1,82t где t=1,2,….год
Найдем тогда скорость роста численности популяции
v(t)= N’(t) = (260*1.82t)’ = 260* (1.82t)’ = 260*1.82t * ln 1.82 (особей/ год)
N0 = 260 особей.
N1(1) = 260*1.821= 260*1.82= 474 особи
N2(2)= 260*1.822= 260*3.3124= 861 особь.
Анализ результата: Наблюдается ежегодный прирост численности популяции. Такие процессы всегда происходят только в благоприятных условиях среды обитания для данной популяции.
Заключение.
Обсуждая успехи своего ученика, учитель математики так отозвался о нем: “Он очень мало знает, но у него положительная производная”. Учитель хотел сказать, что скорость приращения знаний у ученика положительная, а это есть залог того, что знания возрастут.